The development of the Black-Scholes model for pricing options, which revolutionized finance and spawned multiple trillion-dollar industries. The story begins with Louis Bachelier's discovery of the random walk, a mathematical model that describes the movement of stock prices. Bachelier's work, while initially ignored, provided the foundation for future breakthroughs, including Einstein's explanation of Brownian motion. Later, Ed Thorpe, a renowned blackjack player, applied card-counting strategies to the stock market and devised a more accurate option pricing model than Bachelier's. Finally, Black and Scholes developed the iconic Black-Scholes equation, which allowed for precise option pricing and led to the rapid growth of derivatives markets. The exploring the implications of these discoveries, including the potential for market inefficiency and the role of mathematicians and physicists in shaping modern finance.
The Black-Scholes model’s development marks one of finance’s most transformative moments, reshaping the trading of options and laying the groundwork for the vast, complex derivatives markets seen today. The story indeed begins with Louis Bachelier, a largely unrecognized French mathematician who, in 1900, introduced the concept of the random walk in his dissertation *Théorie de la Spéculation.* Bachelier’s work sought to capture the erratic movement of stock prices, and he theorized that prices move in a random fashion, driven by both information and speculation. This revolutionary idea—of stock prices oscillating like particles in a gas—proved invaluable later on, though initially, it was dismissed as unconventional by the academic and financial communities of the time. Notably, Bachelier’s model of price fluctuations went largely unnoticed for several decades, an unfortunate fate shared by many early ideas that were ahead of their time.
It was only after Albert Einstein’s 1905 paper on Brownian motion that Bachelier’s ideas gained renewed interest, though through an indirect route. Einstein, independently from Bachelier, used similar mathematical techniques to explain the random motion of particles suspended in a fluid, a phenomenon now synonymous with the randomness observed in stock price movements. Physicists recognized Brownian motion as a fundamental insight into randomness, and its application to finance emerged gradually as scholars in disparate fields began to link the principles of randomness across disciplines.
A fascinating bridge to modern option pricing came with Edward O. Thorp, an academic turned blackjack player. Thorp, who famously exploited the mechanics of card-counting in blackjack, applied his analytical prowess to finance in the 1960s. In his 1967 book *Beat the Market,* Thorp introduced options pricing models that improved on Bachelier’s theories by accounting for volatility and market dynamics more realistically. Thorp’s insights were groundbreaking: he demonstrated that risk and reward could be calibrated through sophisticated quantitative methods, essentially setting the stage for the formalization of options theory. Unlike Bachelier’s random walk, Thorp’s approach to option pricing directly influenced practitioners and bridged academic theory with practical application, making him a trailblazer in the nascent field of quantitative finance.
The definitive leap came in 1973 when economists Fischer Black and Myron Scholes published the Black-Scholes model, formalizing option pricing in a way that accounted for time decay, volatility, and interest rates in a single equation. Their model introduced the concept of a “hedged position,” where a portfolio of options and their underlying assets could be balanced to eliminate risk, allowing for a theoretically risk-free position. This pivotal insight led to the creation of the now-iconic Black-Scholes equation, an elegant partial differential equation that allowed traders to calculate an option’s fair value based on current market conditions. Though developed with economist Robert Merton’s contributions, Black and Scholes' model crystallized the idea of dynamic hedging and created the mathematical scaffolding for the modern options market.
The practical and economic implications of Black-Scholes were profound. The model allowed traders to standardize pricing, enabling the launch of options exchanges, beginning with the Chicago Board Options Exchange (CBOE) in 1973. This model spurred the growth of the derivatives market, leading to financial instruments whose notional value now exceeds trillions of dollars. Beyond financial innovation, Black-Scholes underscored the intersection of physics, mathematics, and finance, as it attracted academics from hard sciences to Wall Street, eager to leverage their quantitative skills in financial modeling.
However, the model’s assumptions—such as continuous trading, constant volatility, and frictionless markets—have been scrutinized, particularly during financial crises when markets exhibit extreme inefficiencies. Critics argue that Black-Scholes, while mathematically elegant, may oversimplify the chaotic reality of financial markets. Market inefficiencies and irrational behaviors remain, and extreme events like the 2008 financial crisis demonstrated the potential dangers of relying on models that assume rationality and stability.
Despite these criticisms, the Black-Scholes model reshaped finance, elevating mathematics and physics to the forefront of financial theory and practice. Today, quantitative analysts or “quants” are essential to modern finance, building on the foundations set by Bachelier, Einstein, Thorp, and Black-Scholes. Their work continues to influence trading algorithms, risk management practices, and the development of new financial products, proving the lasting impact of a model that began with a simple idea: that randomness can, in fact, be mathematically described.
From Physics to Finance: A History of Options, Risk, and the Quest to Beat the Market
This briefing document reviews the key themes and insights from the provided source material, which explores the fascinating intersection of physics, mathematics, and finance. It delves into the history of options trading, the development of mathematical models to price them, and the role of physicists and mathematicians in revolutionizing financial markets.
Main Themes:
The Intertwined History of Physics and Finance: The development of sophisticated financial models, particularly those related to options pricing, heavily draws upon concepts from physics, particularly statistical mechanics and the study of random processes.
The Role of Randomness and the Efficient Market Hypothesis: A key concept explored is the idea of randomness in market price movements and the challenge of predicting future prices. The Efficient Market Hypothesis posits that in a truly efficient market, all available information is already reflected in prices, making consistent above-average returns impossible.
Evolution of Option Pricing Models: Starting from Bachelier's pioneering work to the groundbreaking Black-Scholes-Merton model, the document traces the evolution of increasingly sophisticated models for accurately pricing options and managing risk.
Impact of Technology and Data Analysis: The rise of powerful computers and sophisticated data analysis techniques, like machine learning, has significantly transformed the financial landscape, enabling firms like Renaissance Technologies to identify hidden patterns and achieve extraordinary returns.
Key Facts and Insights:
The Black-Scholes-Merton Equation: This groundbreaking equation, developed by Fischer Black, Myron Scholes, and Robert Merton, revolutionized options trading by providing a formula to accurately price options based on factors like the underlying asset's price, volatility, and time to expiration.
"For the very first time, you now have an explicit expression where you plug in the parameters and out pops this number so that people can actually use it to trade on."
The Derivatives Market: The development of option pricing models has led to the explosive growth of the derivatives market, which now dwarfs the value of the underlying assets they are based on.
"In general, the size of derivative markets globally is on the order of several hundred trillion dollars."
The Rise of Quantitative Finance: Mathematicians and physicists have become increasingly sought after in the financial industry due to their expertise in probability, statistics, and complex modeling.
"It's not surprising that mathematicians and physicists are involved in this field. First of all, finance pays a lot better than, you know, being an assistant professor of mathematics."
The Challenge to the Efficient Market Hypothesis: The remarkable success of firms like Renaissance Technologies, utilizing advanced mathematical models and data analysis, has led some to question the validity of the Efficient Market Hypothesis.
"In 1988, I published a paper testing it, the US Stock Market, and what I found was that the hypothesis is false. You can actually reject the hypothesis in the data. And so there are predictabilities in the stock market."
Quotes from the Source Material:
On the obscurity of Bachelier's work: "When Bachelier finished his thesis, he had beaten Einstein to inventing the random walk and solved the problem that had eluded options traders for hundreds of years. But no one noticed. The physicists were uninterested and traders weren't ready."
On the power of options: "These pieces of paper that we call options and derivatives, they basically allow us to create many, many different versions of the underlying asset, versions that individuals find more palatable because of their own risk reward preferences."
On the potential destabilizing effects of derivatives: "During abnormal times, by that I mean when there are periods of market stress, all of these securities can go in one direction, typically down, and when they go down together, that creates a really big market crash."
On the goal of Renaissance Technologies: "The real thing was to gather a tremendous amount of data and we had to get it by hand in the early days, we went down to the Federal Reserve and copied interest rate histories and stuff like that 'cause it didn't exist on computers."
Conclusion:
The source material provides a compelling historical account of how concepts from physics and mathematics have revolutionized financial markets. From the development of sophisticated option pricing models to the rise of quantitative finance, the influence of these disciplines is undeniable. It also raises thought-provoking questions about the nature of market efficiency and the ongoing quest to identify and exploit patterns in the seemingly chaotic world of finance.
FAQ: The Mathematics of the Market
1. What is the Black-Scholes-Merton model and why is it important?
The Black-Scholes-Merton (BSM) model is a mathematical equation used to price options, which are financial contracts that give the holder the right, but not the obligation, to buy or sell an asset at a specific price in the future. The model revolutionized finance by providing a way to accurately and efficiently price these complex instruments. Its importance lies in its widespread adoption by the financial industry, leading to the explosive growth of multi-trillion dollar derivatives markets like options, credit default swaps, and securitized debt.
2. What is an option, and how does it work?
An option is a financial contract that grants the holder the right, but not the obligation, to buy (call option) or sell (put option) an asset at a predetermined price (strike price) on or before a specific date (expiration date). For example, if you buy a call option for Apple stock at a strike price of $150, and the stock price rises above $150 before the expiration date, you can exercise your option to buy the stock at the lower strike price and sell it at the higher market price, making a profit.
3. How did Bachelier contribute to the understanding of financial markets?
Louis Bachelier, a French mathematician, is considered the pioneer of using mathematics to model financial markets. In his 1900 PhD thesis, he introduced the concept of the random walk to describe stock price movements, arguing that prices are equally likely to go up or down, making them unpredictable in the short term. This laid the groundwork for future models like the BSM model and significantly advanced the understanding of market dynamics.
4. What is the Efficient Market Hypothesis and how does it relate to option pricing?
The Efficient Market Hypothesis (EMH) states that asset prices fully reflect all available information, making it impossible to consistently beat the market. This implies that any attempt to predict future prices based on past data or analysis is futile. In the context of option pricing, the EMH suggests that options are fairly priced, meaning both buyers and sellers have an equal chance of profit. However, the success of quantitative hedge funds like Renaissance Technologies, which use complex mathematical models to exploit market inefficiencies, challenges the validity of the EMH.
5. How did Jim Simons and Renaissance Technologies revolutionize the investment world?
Jim Simons, a mathematician and founder of Renaissance Technologies, pioneered the use of machine learning and quantitative analysis in financial markets. He hired experts in fields like physics, mathematics, and signal processing to develop sophisticated algorithms that identify patterns in vast amounts of data, enabling the firm's Medallion fund to achieve extraordinary returns. Their success demonstrates the potential of applying advanced mathematical and computational techniques to uncover market inefficiencies and generate consistent profits.
6. What are the potential risks and benefits of derivatives markets?
Derivatives markets can contribute to both market stability and instability. During normal times, they provide liquidity and hedging opportunities, allowing investors to manage risk effectively. However, during periods of market stress, the interconnected nature of these markets can amplify losses and contribute to rapid market downturns. For example, the widespread use of credit default swaps played a role in the 2008 financial crisis.
7. How can options be used to hedge against risk?
Options offer a way to mitigate specific financial risks. For instance, an airline concerned about rising fuel prices can buy call options on oil. If oil prices increase, the option will gain value, offsetting the airline's increased fuel costs. Similarly, a farmer worried about falling crop prices can buy put options, which will generate profits if prices decline, protecting against potential losses.
8. How has the understanding of randomness and patterns in financial markets evolved?
The evolution of understanding randomness and patterns in financial markets has been driven by contributions from mathematicians and physicists. Early work by Bachelier introduced the concept of the random walk, suggesting inherent unpredictability in stock prices. Later, Black, Scholes, and Merton developed a mathematical model to price options based on the assumption of randomness and efficient markets. However, the success of quantitative hedge funds like Renaissance Technologies, which exploit complex patterns in data, challenges the notion of complete randomness and raises questions about the absolute efficiency of markets. The ongoing pursuit of uncovering patterns and understanding their interplay with randomness continues to shape the evolution of financial theory and practice.
A Deep Dive into the World of Derivatives and Market Dynamics
Quiz
What mathematical concept did Louis Bachelier apply to financial markets, and how did it contribute to his groundbreaking work on option pricing?
Explain the concept of dynamic hedging and how it allows for the creation of synthetic options.
What key improvements did Ed Thorpe make to Bachelier's model for pricing options, and how did he apply his knowledge of gambling to financial markets?
Describe the fundamental principle behind the Black-Scholes-Merton equation and its impact on the options trading industry.
How did the Black-Scholes-Merton equation revolutionize hedging strategies beyond the realm of hedge funds? Provide an example.
Briefly discuss the role of options in the GameStop short squeeze of 2021 and the leverage they provided to retail investors.
What is the estimated size of the global derivatives market compared to the underlying assets they are based on? Explain why this discrepancy exists.
Outline the contrasting effects of derivatives markets on global economic stability during periods of normalcy and market stress.
What unique approach did Jim Simons bring to Renaissance Technologies, and what was his rationale for believing that this approach could outperform the market?
Explain how the success of the Medallion Fund, managed by Renaissance Technologies, challenged the Efficient Market Hypothesis. What are the implications of this challenge?
Answer Key
Bachelier applied the concept of the random walk to stock prices, assuming they were equally likely to go up or down. This formed the basis of his model for calculating the expected return of an option, leading to a method for determining its fair price.
Dynamic hedging involves continuously adjusting a portfolio of options and the underlying asset to offset potential losses. This allows for the creation of synthetic options where the seller mimics the payoff of a real option without actually owning it.
Thorpe recognized that stock prices weren't entirely random and incorporated drift, the tendency for prices to trend upwards or downwards, into his model. He applied his card-counting skills from blackjack to identify and exploit market inefficiencies, demonstrating the potential for mathematical strategies in finance.
The Black-Scholes-Merton equation assumes that a risk-free portfolio of options and stocks should only return the risk-free rate. By combining this principle with a model for stock price fluctuations, they derived a formula to calculate the fair price of any option, revolutionizing the industry and establishing a standardized pricing method.
The equation enabled the accurate and efficient hedging of various risks, extending beyond hedge funds to large corporations, governments, and individual investors. For example, airlines can hedge against rising oil prices by purchasing options on oil-related assets.
Retail investors on Reddit utilized options, particularly call options, to amplify their buying power during the GameStop short squeeze. The inherent leverage of options allowed them to control a larger number of shares than their capital would normally permit, contributing to the rapid price surge and losses for short sellers.
The global derivatives market is estimated to be worth several hundred trillion dollars, exceeding the value of the underlying assets by multiples. This discrepancy arises from the ability of derivatives, such as options, to create numerous variations of the underlying asset, catering to diverse risk appetites and investment strategies.
During stable market conditions, derivatives provide liquidity and facilitate risk management, enhancing overall stability. However, during periods of market stress, the interconnected nature of derivatives can trigger cascading losses, amplifying market volatility and potentially exacerbating financial crises.
Simons employed machine learning to uncover hidden patterns within vast amounts of financial data. His experience in code-breaking during the Cold War led him to believe that similar data-driven approaches could identify predictable patterns and exploit market inefficiencies.
The Medallion Fund's consistent outperformance over decades challenged the Efficient Market Hypothesis, which posits that stock prices fully reflect all available information, making it impossible to consistently beat the market. The fund's success suggests that certain market inefficiencies may exist, and sophisticated models can potentially identify and capitalize on them.
Essay Questions:


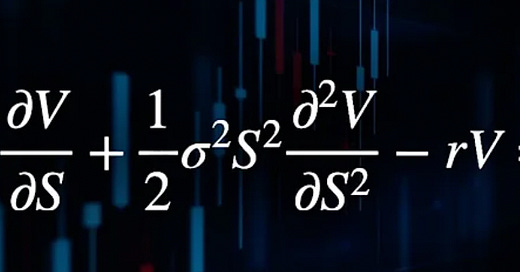












Share this post